Introduction to LibAUC

by Zhuoning Yuan and Tianbao Yang

Overview

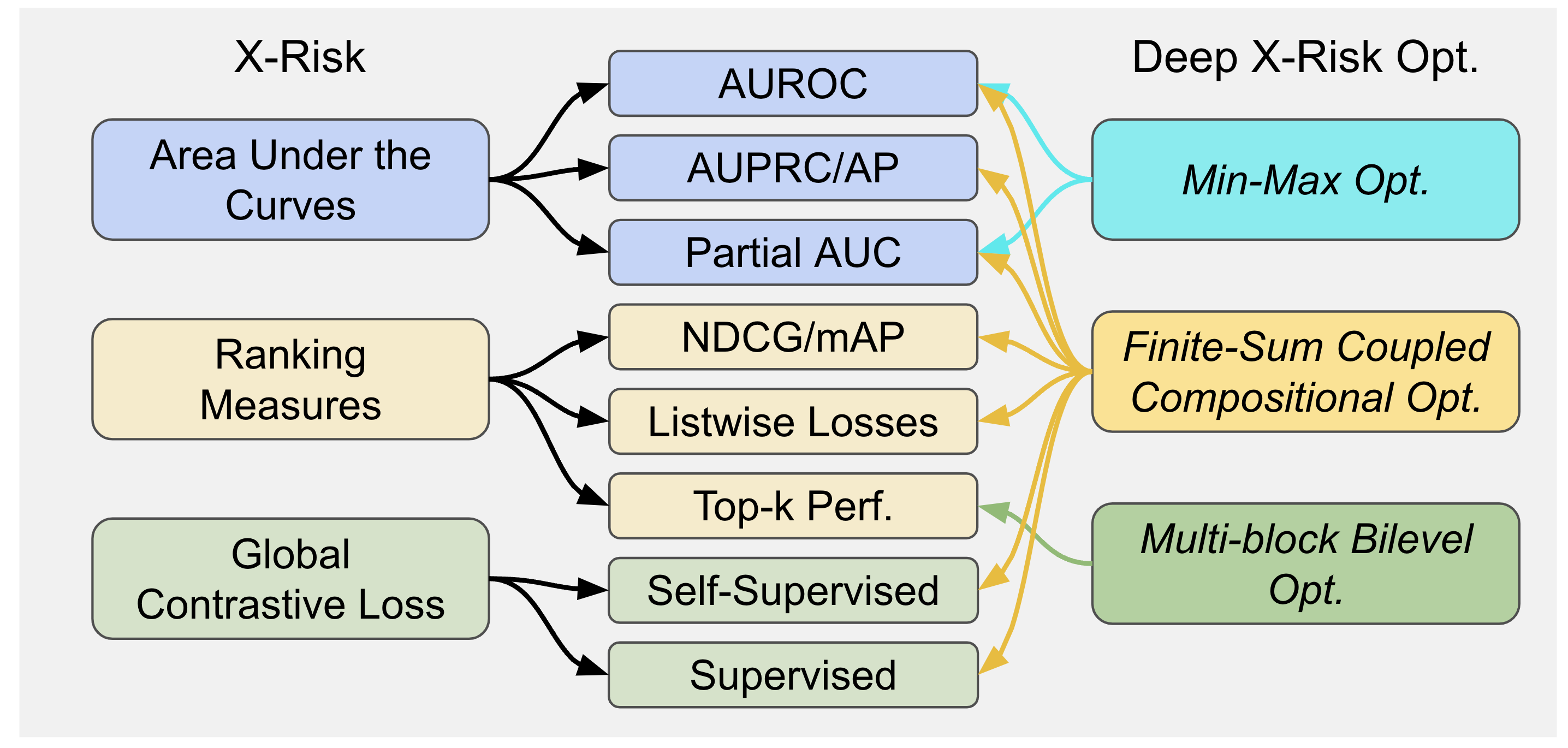
Traditional risk functions such as the cross-entropy loss, are limited in modeling a wide range of problems or tasks, e.g., classification with imbalanced data (CID), learning to rank (LTR), contrastive learning of representations (CLR). X-risk refers to a family of compositional measures in which the loss function of each data point is defined in a way that contrasts the data point with a large number of others. It covers a family of widely used measures/losses including but not limited to the following three interconnected categories:

• Areas Under the Curves, including areas under ROC curves (AUROC), areas under Precision-Recall curves (AUPRC), one-way and two-wary partial areas under ROC curves.

• Ranking Measures/Objectives, including p-norm push for bipartite ranking, listwise losses for learning to rank (e.g., listNet), mean average precision (mAP), normalized discounted cumulative gain (NDCG), etc.

• Contrastive Objectives, including supervised contrastive objectives (e.g., NCA), and global self-supervised contrastive objectives improving upon SimCLR and CLIP.

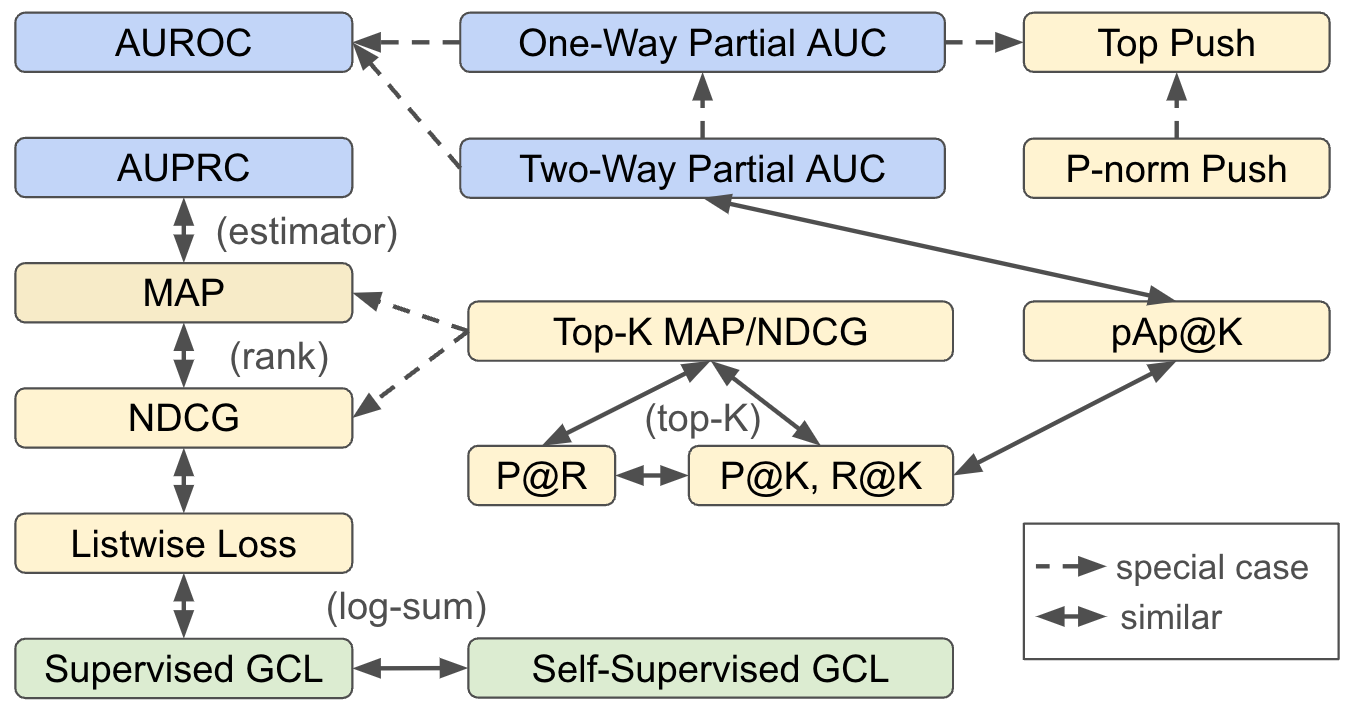
Relationships between X-Risks

The following figure demonstrates the relationships between different X-risks. AUROC is a special case of one-way pAUC and two-way pAUC. One-way pAUC with FPR in a range \((0, \alpha)\) is a special case of two-way pAUC. Top Push is a special case of one-way pAUC and p-norm push. AP is a non-parametric estimator of AUPRC. MAP and NDCG are similar in the sense that they are functions of ranks. Top-K MAP, Top-K NDCG, Recall@K (R@K), Precision@K (P@K), partialAUC+Precision@K (pAp@K), Precision@Recall (P@R) are similar in the sense that they all involve the computation of K-th largest scores in a set. Listwise losses, supervised contrastive losses, and self-supervised contrastive losses are similar in the sense that they all involve the sum of log-sum term.

Mathematical Definition & Optimization Challenges

The mathematical formulation behind X-Risk Optimization is defined as follows:

\[\min _{\mathbf{w} \in \mathbb{R}^d} F(\mathbf{w})=\frac{1}{|\mathcal{S}|} \sum_{\mathbf{z}_i \in \mathcal{S}} f_i\left(g\left(\mathbf{w}; \mathbf{z}_i, \mathcal{S}_i\right)\right)\]

The gradient of the above objective involves computing \(\nabla f_i(g(\mathbf{w}, \mathbf{z}_i, \mathcal{S}_i))\nabla g(\mathbf{w}, \mathbf{z}_i, \mathcal{S}_i)\). The challenge of computing this gradient lies at (i) the inner function \(g(\mathbf{w}, \mathbf{z}_i, \mathcal{S}_i)\) and its gradient \(\nabla g(\mathbf{w}, \mathbf{z}_i, \mathcal{S}_i)\) are not easy to compute since \(\mathcal{S}_i\) could be a large set; (ii) the gradient of inner function \(\nabla g(\mathbf{w}, \mathbf{z}_i, \mathcal{S}_i)\) might also involve implicit gradient. Hence, proper estimators for \(g(\mathbf{w}, \mathbf{z}_i, \mathcal{S}_i)\) and \(\nabla g(\mathbf{w}, \mathbf{z}_i, \mathcal{S}_i)\) are needed to ensure the convergence of optimization. As a result, the training pipeline for X-risk optimization needs to be designed specially to ensure the algorithms converge.

LibAUC Training Pipeline

The LibAUC training pipeline is shown below. It has two unique components, namely Controlled Data Sampler and Dynamic Mini-batch Loss, which are highlighted in yellow.

Loss & Optimizer

We present a list of names of dynamic losses, their corresponding controlled data samplers and optimizer wrappers in the LibAUC library, along with references in the following Table.

Loss Function	Data Sampler	Optimizer Wrapper	Reference
AUCMLoss	DualSampler	PESG	yuan2021large
CompositionalAUCLoss	DualSampler	PDSCA	yuan2022compositional
APLoss	DualSampler	SOAP	qi2021stochastic
pAUCLoss(‘1w’)	DualSampler	SOPAs	zhu2022auc
pAUCLoss(‘2w’)	DualSampler	SOTAs	zhu2022auc
MultiLabelAUCMLoss	TriSampler	PESG	yuan2023libauc
mAPLoss	TriSampler	SOTAs	yuan2023libauc
MultiLabelpAUCLoss	TriSampler	SOPAs	yuan2023libauc
NDCGLoss	TriSampler	SONG	qiu2022largescale
NDCGLoss(topk=5)	TriSampler	SONG	qiu2022largescale
ListwiseCELoss	TriSampler	SONG	qiu2022largescale
GCLoss(‘unimodal’)	RandomSampler	SogCLR	yuan2022provable
GCLoss(‘bimodal’)	RandomSampler	SogCLR	yuan2022provable
GCLoss(‘unimodal’, enable_isogclr=True)	RandomSampler	iSogCLR	qiu2023provable
GCLoss(‘bimodal’, enable_isogclr=True)	RandomSampler	iSogCLR	qiu2023provable
MIDAMLoss(‘attention’)	DualSampler	MIDAM	zhu2023provable
MIDAMLoss(‘softmax’)	DualSampler	MIDAM	zhu2023provable

Achievements

LibAUC has made significant strides in advancing research and industry standards. Here are the major achievements of our work:

• 3+ Challenge-winning Solutions: LibAUC techniques have empowered researchers to win several competitions.

• 4+ Industrial Collaborations: Our tools have been successfully applied to real-world industrial problems.

• 25+ Scientific Publications: LibAUC’s contributions have fostered significant academic progress.

• 37,000+ downloads Worldwide: LibAUC’s global recognition is demonstrated by its extensive downloads worldwide.

History of LibAUC

The development of the library originated from a project in the OptMAI Lab at the University of Iowa, led by Zhuoning Yuan under the supervision of Dr. Tianbao Yang, focusing on deep AUROC maximization. Zhuoning made original and significant contributions by achieving 1st place in the Stanford CheXpert Competition in 2020, demonstrating the success of deep AUROC maximization. This success prompted the decision to develop the library, which is why it is named the LibAUC library. The first version was released in Spring 2021.

In Spring 2021, the OptMAI lab collaborated with Dr. Shuiwang Ji’s research group to explore deep AUPRC maximization for improving classification performance in the MIT AICURES Challenge. Later, the finite-sum coupled compositional optimization framework for AUPRC maximization was extended to solving a broad range of problems. Additionally, multi-block bilevel optimization techniques were introduced for optimizing top-K performance measures.

In June 2022, a major update was implemented, incorporating optimization algorithms for AP, NDCG, partial AUC, and global contrastive loss into the library. During this period, Dixian Zhu, Gang Li, and Zi-Hao Qiu joined the development team, with Zhuoning Yuan continuing to lead the development. In Summer 2022, the OptMAI lab moved to Texas A&M University, and Yang introduced the generic X-risk optimization framework, expanding the library’s scope from AUC maximization to X-risk optimization. However, the name LibAUC was retained.

In June 2023, the team conducted another significant update to the library, including enhancements to the codebase, launch of a new documentation website and the debut of a redesigned logo. This release also incorporated two additional algorithms to the library, namely iSogCLR for contrastive learning, and MIDAM for multi-instance deep AUC maximization.

Acknowledgments

Acknowledgments go to other students who made original contributions, such as Qi Qi, who conducted early studies on AP maximization, Bokun Wang, who improved convergence analysis of finite-sum coupled compositional optimization, Zhishuai Guo, who contributed original convergence analysis of compositional AUROC maximization, and Quanqi Hu, who performed original convergence analysis of multi-block bilevel optimization.

Recognition is also given to previous lab members, including Dr. Mingrui Liu, who conducted original analysis of minimax optimization for AUROC maximization, Dr. Yan Yan, who simplified the minimax optimization algorithms and improved their analysis, and Yongjian Zhong, who conducted some experiments.

The team expresses gratitude to collaborators, including Dr. Milan Sonka (IEEE Fellow, University of Iowa), Dr. Nitesh Chawla (IEEE Fellow, ACM Fellow, University of Notre Dame), Dr. Shuiwang Ji (IEEE Fellow, Texas A&M University), Dr. Jiebo Luo (IEEE Fellow, ACM Fellow, University of Rochester), Dr. Xiaodong Wu (University of Iowa), Dr. Qihang Lin (University of Iowa), Dr. Yiming Ying (University at Albany), Dr. Denny Zhou (Google Brain), Dr. Xuanhui Wang (Google), Dr. Rong Jin (Alibaba Group), Dr. Yi Xu (Alibaba Group), Dr. Yuexin Wu (Google), Dr. Xianzhi Du (Google), Dr. Lijun Zhang (Nanjing University), Yao Yao (University of Iowa), Guanghui Wang (Georgia Tech), Youzhi Luo (Texas A&M University), Zhao Xu (Texas A&M University).

The OptMAI Lab will continue to maintain and update the library. We welcome students and researchers to collaborate on this exciting journey.